Translate this page into:
Comparison of Formula-Based Methods with Diverse TGL: VLDL-C Ratio for Calculating LDL-C in a Tertiary Care Hospital
Address for correspondence: Maneni V. P. Chowdary, PhD, Department of Biochemistry, KMCH Institute of Health Sciences & Research, Coimbatore, Tamil Nadu, 641014, India (e-mail: chowdarymvp@gmail.com).
This article was originally published by Thieme Medical and Scientific Publishers Pvt. Ltd. and was migrated to Scientific Scholar after the change of Publisher.
Abstract
Background
The most popular Friedewald formula (FF) was tailored with a fixed factor of 5 for triglyceride-very low-density lipoprotein cholesterol (TGL:VLDL-C) ratio. Some of the subsequent studies on diverse population demonstrated modified FF with only altered TGL:VLDL-C ratio, comprising either a fixed or an adjustable factor. Hata and Nakajima as well as Puavilai et al proposed fixed factors of 4 and 6, respectively. Recently, Martin et al recommended an adjustable factor derived as N-strata-specific median TGL:VLDL-C ratio based on TGL and non-high-density lipoprotein cholesterol (non-HDL-C).
Aim
This comparative retrospective study evaluates the efficacy of LDL-C formulae, varying only in TGL-VLDL-C ratio, using direct LDL-C assay as a reference method in a tertiary care hospital.
Materials and Methods
A total of 1,747 patient records with lipid profile data were procured. Concordance analysis, absolute difference, and post hoc test were employed as analytical tools. The impact of total cholesterol (TChol), TGL, and HDL-C on formulae was also evaluated.
Results
Overall, Martin equation had relatively the highest concordance, narrowest absolute difference, and minimal influence of TChol, TGL, and HDL-C. On the contrary, the Hata method revealed comparatively the lowest concordance, widest absolute difference, and high influence of TChol, TGL, and HDL-C. The remaining formula-based approaches, that is, FF and Puavilai calculation, executed mostly inconsistent intermittent features between Martin equation and Hata method.
Conclusion
Relatively dominant and competitive analytical attributes of the Martin equation with an adjustable TGL:VLDL-C factor outweigh the remaining three formulae-based methods with fixed TGL:VLDL-C factor in Indian adults.
Keywords
total cholesterol
triglycerides
low-density lipoprotein cholesterol
high-density lipoproteins cholesterol
Very low-density lipoprotein cholesterol
Introduction
As low-density lipoprotein cholesterol (LDL-C) dictates diagnosis, risk classification, and treatment of cardiovascular disease in both national and international practice guidelines,[1,2] accurate quantitative estimation of its blood level is imperative. Beta (β) quantification based on ultracentrifugation is a gold standard method. However, inherent limitations of β-quantification hindered its establishment as routine diagnostic setup.[3] Though homogenous assays evolved as feasible alternative, yet its exorbitant feature among lipid profile assays widens the financial burden on patient. Hence, in developing countries like India, its quantification remained ambiguous and instead Friedewald formula (FF) is adopted.[3] Since its exploration, this formula has successfully established and been broadly utilized as an economical alternative method in most of the diagnostic laboratories irrespective of its restricted recommendations.
FF was depicted on a presumption that triglyceride to very low-density lipoprotein cholesterol (TGL:VLDL-C) ratio remains constant as 5:1 under fasting conditions. In the subsequent studies, Hata and Nakajima[4] and Puavilai et al[5] demonstrated the effectiveness of a constant factor of 4 and 6, respectively. However, fixing a constant factor even in fasting conditions not only compromises the variance in TGL:VLDL-C across the TGL and non-high-density lipoprotein-cholesterol (non-HDL-C) range but also the interindividual variances in TGL:VLDL-C ratio. In one of the latest studies, to minimize these limitations, Martin et al designed 180-cell table with an adjustable factor derived as N-strata-specific median TG:VLDL-C ratio based on TGL and non-HDL-C.[6] Most of these formulae are derived and validated from respective local populations but only few of them are validated on different races also.[7-19] A major disadvantage in formula-based LDL-C estimations is that their inherent variability is a cumulative product of total cholesterol (TChol), TGLs, and HDL-C assays. As per National Cholesterol Education Program (NCEP) expert panel report, the variability encountered in routine laboratories (~12%) was higher than well-standardized lipid laboratories (~4%).[20]
Growing body of evidence demonstrates the entwined impact of dietary supplements of various races on lipid profile.[21,22] Therefore, contemplation of any novel approach in clinical setup warrants prior rigorous validation under different laboratory conditions and in an independent population of various races. In previous studies on Indian population, the various combinations of correlation, paired t-test, regression, and Bland-Altman difference plot analyses were adopted as statistical tools to understand the agreement of either (or) both FF and modified FF methods with direct LDL-C (LDL-C) measurements.[15-21] Even in our previous study, Bland-Altman and Lin concordance regression analysis were employed for the evaluation of FF and Martin equation.[15] However, accumulating data of evidence demonstrates the limitations of each of these approaches to quantify agreement in method comparison studies.[23,24] In view of that, the present study was undertaken with an objective to compare the performance of FF, Hata, Puavilai, and Martin method using LDL-CD as reference method. The formula-based LDL-C computations were segregated as per the National Cholesterol Education Program-Adult Treatment Panel III (NCEP-ATP III) guidelines using LDL-CD as the gold standard method. To quantify the performance, interpretations of these formulae using gold standard LDL-CD method were subjected to cross-tabulations to evaluate in terms of concordance and discordance percentages. The absolute difference analysis was employed to understand the extent of variations from LDL-CD. To our knowledge, this is the first comparative study on Indian population employing various formulae-based methods with different TGL:VLDL-C ratio.
Materials and Methods
Ethical Approval
A total of 1,747 medical records of patients comprising lipid profile assay were procured at Karpagam Faculty of Medical Sciences & Research, Coimbatore, Tamil Nadu, India. Permission from the Institutional Human Ethical Committee (IHEC) was obtained for the study design. As it is a retrospective study, IHEC has waived the requirement of informed consent.
Study Participants
The lipid profile data was acquired from July 2016 to June 2017 from the clinical biochemistry laboratory records, Karpagam Faculty of Medical Sciences & Research, Coimbatore, Tamil Nadu, India. Demographic features, anthropometric measurements, and clinical data were extracted from the medical records of the respective patients. According to the medical records, approximately 84.8% of the lipid profile reports pertain to outpatient department subjects enrolled for master-checkup.
The exclusion criteria comprise patients diagnosed with cancer, myocardial infarction, stroke, heart failure, on lipid lowering drugs and lipid profile data comprising TGL greater than 400 mg/dL. The records of participants evident with pregnancy or pregnant on the day of registration were also not included. Only the subjects above18 years of age were recruited in this study.
Biochemical Examination
Fresh venous blood was collected in tubes without anticoagulant from the subjects after an overnight fast. The specimens were allowed to clot for 30 minutes at room temperature and the serum was separated after centrifugation at 3,000 rpm for 15 minutes. The serum lipid profile parameters, that is, TChol, TGL, HDL-C, and LDL-CD, were analyzed within half an hour on EM 360 Clinical Chemistry Analyzer, (TransAsia Bio-Medicals Ltd, Mumbai, Maharashtra, India) using Erba Mannheim XL System Packs. The linearity (intraassay coefficients) of TChol, TGL, HDL-C, and LDL-CD assays were 4.2 to 695 mg/dL (0.98–1.21%), 9.74 to 1062 mg/dL (0.48–0.86%), 1.90 to 193 mg/dL (1.32–1.95%), and 2.60 to 263 mg/dL (1.74–2.16%), respectively. The intraassay coefficients observed in our analysis were in concurrence with manufacturer's measurements. A robust routine “Internal Quality Assurance Program” (Bio-Rad Laboratories Pvt. Ltd, India) and also “External Quality Assurance Program” (Bio-Rad's EQAS program, Bio-Rad Laboratories Pvt. Ltd, India) are a part of our laboratory measures followed not only to meet accreditation requirements but also to provide clinically relevant accurate and precise measurements. The two levels of internal quality controls (normal and pathological) are routinely processed every 24 hours. The results are interpreted daily and periodically via Levey Jennings graph. The lipid profile parameters were calibrated systematically and periodically, that is, generally once in 2 weeks. The laboratory external quality control is performed every month. The entire process of sample collection, processing, and analysis were strictly performed under aseptic conditions as per standard laboratory protocols. After acquiring the lipid profile report of each participant, non-HDL-C and formula-based LDL-C were calculated. Non-HDL-C was derived by subtracting HDL-C from TC. LDL-C using Hata (LDL-CH), FF (LDL-CF), and Puavilai (LDL-CP) were calculated as [non-HDL-C]–[TG/4], [non-HDL-C]–[TG/5], and [non-HDL-C]–[TG/6], respectively. The LDL-C via Martin method (LDL-CM) was computed as [non-HDL-C]–[TG/AF] where AF is an adjustable factor extracted from their recommended 180-cell table.
Statistical Analysis
The acquired lipid profile data was organized and analyzed using Microsoft Excel sheet 2016, and Statistical Package for Social Science (SPSS) version 24 software (Chicago, Illinois, United States). Kolmogorov–Smirnov with Lilliefors significance correction, skewness, and kurtosis was used for assessing normal distribution of the data. Normally distributed continuous variables were presented as mean with standard deviation. Not normally distributed variables were summarized as a median with an interquartile range (IQR). Categorical variables were described as numbers and percentages. Spearman correlation coefficient (ρ) was computed only for understanding the linear association between LDL-CD and formulae-based methods. The concordance of formulae-based LDL-C (LDL-CF, LDL-CH, LDL-CP, and LDL-CM) using LDL-CD as a reference method was classified as per the guidelines of NCEP-ATP III with cutoff of 70, 100, 130, 160, and 190 mg/dL, respectively. Cross-tabulations were generated for concordance in classification between LDL-CD and formulae-based LDL-C (LDL-CF, LDL-CH, LDL-CP, and LDL-CM). Post hoc chi-squared test (Χ2) with Bonferroni adjustment was used for understanding the concordance percentage difference in multiple pairwise comparisons. To understand the difference between formulae-based LDL-C approaches and LDL-CD, absolute difference was computed. Absolute difference was presented as median with an interpercentile range encompassing 5th and 95th percentile. The concordance classified groups of formulae-based LDL-C measurements (LDL-CF, LDL-CH, LDL-CP, and LDL-CM) were segregated in accordance with NCEP-ATP III cutoff of TGL, TChol, and HDL-C. The impact of TGL, TChol, and HDL-C on formulae-based LDL-C measurements was analyzed using absolute difference and Cochran's Q test with post hoc Dunn's test. A two-sided p < 0.05 was considered significant for all analyses.
Results
The general characteristics of the subject's lipid profile recruited in the present study were apparent in ►Table 1A and ►Supplementary Table 1 (available online only). The median age was 49 years with an IQR of 40 to 57 years. Out of 1,747 reports, males comprised 55.1% (962) and females constituted 44.9% (783). The mean of total cholesterol was 201 mg/dL ranging from 156 to 246 mg/dL. TGLs and HDL-C exhibited median (IQR) of 113 mg/dL (83–156 mg/dL) and 40 mg/dL (33–48 mg/dL), respectively. The mean of LDL-CD was 130 mg/dL with a range of 92 to 168 mg/dL. The computed median of LDL-CF, LDL-CH, LDL-CP, and LDL-CM was 133, 127, 137, and 135 mg/dL with an IQR of 104 to 161 mg/dL, 98 to 155 mg/dL, 108 to 166 mg/dL, and 106 to 162 mg/dL, respectively. A very strong correlation coefficient of all formulae (LDL-CM = LDL-CP > LDL-CF > LDL-CH) against LDL-C was observed (►Table 1B, ►Supplementary Fig. 1 [available online only]).
| Variables | Total |
|---|---|
| Age, y | 49 (40–57) |
| Sex, n (%) | |
| Male | 962 (55.1%) |
| Female | 783 (44.9%) |
| Total cholesterol (TChol), mg/dL | 201 ± 45 |
| Triglycerides (TGL), mg/dL | 113 (83–156) |
| High-density lipoprotein cholesterol (HDL-C), mg/dL | 40 (33–48) |
| Low-density lipoprotein (LDL-C), mg/dL | |
| Directly measured LDL-C (LDL-CD), mg/dL | 130 ± 38 |
| Friedewald (LDL-CF), mg/dL | 133 (104–161) |
| Hatta (LDL-CH), mg/dL | 127 (98–155) |
| Puavilai (LDL-CP), mg/dL | 137 (108–166) |
| Martin (LDL-CM), mg/dL | 135 (106–162) |
Abbreviations: LDL-CD, direct LDL-C assay; LDL-CF, Friedewald LDL-C calculation; LDL-CH, Hata LDL-C calculation; LDL-CP, Puavilai LDL-C calculation; LDL-CM, Martin LDL-C calculation.
Normally distributed data was expressed as mean ± standard deviation, nonnormal distributed data as median (interquartile range), and categorical variables as number (percent).
| Direct LDL-C vs. Formula based method | Correlation coefficient (ρ) |
|---|---|
| LDL-CD vs. LDL-CF | 0.972 |
| LDL-CD vs. LDL-CH | 0.964 |
| LDL-CD vs. LDL-CP | 0.975 |
| LDL-CD vs. LDL-CM | 0.975 |
Abbreviations: LDL-C, low-density lipoprotein cholesterol; LDL-CD, Direct LDL-C assay; LDL-CF, Friedewald LDL-C calculation; LDL-CH, Hata LDL-C calculation; LDL-CM, Martin LDL-C calculation; LDL-CP, Puavilai LDL-C calculation.
The concordances between LDL-C and formulae-based LDL-C estimates segregated as per the NCEP-ATP III guideline were evident in ►Table 2, ►Supplementary Tables 2 and 3 and ►Supplementary Fig. 2 (available online only). Both formulae with extreme end fixed factors, that is, LDL-CP with highest fixed factor & LDL-CH with lowest fixed factor exhibited significant differences with respect to each other at each stipulated interval of LDL-C. The relative concordance percentages of LDL-CP at the lower end of LDL-C intervals comprised highest at 70 to 99 mg/dL, higher at < 70 mg/dL, and high at 130 to 159 mg/dL. On the other side, LDL-CH exhibited highest concordance percentage in the remaining intervals of LDL-C (130–159 mg/dL, 160–189 mg/dL, and ≥ 190 mg/dL). In the same perspective, the distribution of relative concordance percentage of novel LDL-CM with an adjustable fixed factor at various LDL-C intervals was highest at < 70 mg/dL as well as 100 to 129 mg/dL and high at 130 to 159 mg/dL, whereas higher in the remaining intervals. Finally, the most widely adopted LDL-CF with an intermittent fixed factor had higher concordance percentage only at LDL-C intervals comprising 100 to 129 and 130 to 159 mg/dL. In the remaining intervals of LDL-C, it has restricted itself with relatively high concordance percentage. All the formulae-based methods with highest, higher, and high concordance percentages were in mutual concurrence to each other without any significant difference at every restricted interval of LDL-C. Only at LDL-C interval of 160 to 189 mg/dL, LDL-CF exhibited significant disparity with LDL-CH. On a cumulative basis encompassing the entire pooled data, the concordance percentage of LDL-CM > LDL-CF > LDL-CH > LDL-CP, where concordance percentage difference between LDL-CM and LDL-CF was not significant. The relative dominance of LDL-CM could be attributed to its highest concordance percentage and also especially higher-to-high concordance percentage without any significant difference relative to highest concordance percentage possessing formulae-based methods at stipulated LDL-C interval.
| LDL-CF | LDL-CH | LDL-CP | LDL-CM | |||||
|---|---|---|---|---|---|---|---|---|
| C/T | %(95%CI) | C/T | %(95%CI) | C/T | %(95%CI) | C/T | %(95%CI) | |
| LDL-C, mg/dL | ||||||||
| < 70 (n = 95) | 82/107 | 76.6 (68.6–84.6) | 86/137 | 62.8 (54.7–70.9) | 75/88 | 85.2 (77.8–92.6) | 76/89 | 85.4 (78.0–92.7) |
| 70–99 (n = 279) | 224/277 | 80.8 (76.2–85.5) | 220/324 | 67.9 (62.8–72.9) | 204/229 | 89.0 (85.0–93.1) | 226/255 | 88.6 (84.7–92.5) |
| 100–129 (n = 484) | 350/419 | 83.5 (79.9–87.1) | 348/469 | 74.2 (70.2–78.2) | 342/417 | 82.0 (78.3–85.7) | 367/434 | 84.6 (81.2–88.0) |
| 130–159 (n = 515) | 380/487 | 78.0 (74.3–81.7) | 349/434 | 80.4 (76.7–84.1) | 357/496 | 72.0 (68.0–75.9) | 389/502 | 77.5 (73.8–81.1) |
| 160–189 (n = 270) | 187/284 | 65.8 (60.3–71.4) | 193/253 | 76.3 (71.0–81.5) | 162/310 | 52.2 (46.7–57.8) | 201/301 | 66.8 (61.4–72.1) |
| ≥ 190 (n = 104) | 102/173 | 58.9 (51.6–66.3) | 94/130 | 72.3 (64.6–79.9) | 103/207 | 49.7 (42.9–56.6) | 103/166 | 62.0 (54.7–69.4) |
| Overall | 1325/1747 | 75.8 (73.7–77.8) | 1290/1747 | 73.8 (71.7–75.8) | 1243/1747 | 71.1 (68.9–73.2) | 1362/1747 | 77.9 (75.9–79.8) |
Abbreviations: C/T, concordant number/total number; CI, confidence interval. Concordance was designated in accordance to direct LDL-C; LDL-C, low-density lipoprotein cholesterol; LDL-CF, Friedewald LDL-C; LDL-CH, Hata LDL-C; LDL-CM, Martin LDL-C; NCEP-ATPIII, National Cholesterol Education Program-Adult Treatment Panel III; LDL-CP, Puavilai LDL-C.
As apparent from ►Fig. 1 and ►Supplementary Table 2 (available online only), the overall discordant percentage of LDL-CP > LDL-CH > LDL-CF > LDL-CM. The overestimation and underestimation proportions comprising the discordant percentage of LDL-CP > LDL-CM > LDL-CF > LDL-CH and LDL-CH > LDL-CF > LDL-CM > LDL-CP, respectively. These interpretations are apparent even at each clinically demarcated interval of LDL-C with minor interchanging positions. Dominance of underestimation in LDL-C and overestimation in the remaining formulae emerged as characteristic features of the respective approaches. A gradual escalation of their characteristic discordant percentage was apparent with increasing levels of LDL-C. Even the absolute difference analysis observations are also in consensus with output of discordant percentage computations (►Supplementary Fig. 3 [available online only]). LDL-CM has relatively narrowest interpercentile range at both comprehensive and in stipulated intervals of LDL-C. LDL-CH, on contrary, has widest interpercentile range. The remaining two formulae exhibited mostly intermittent features.
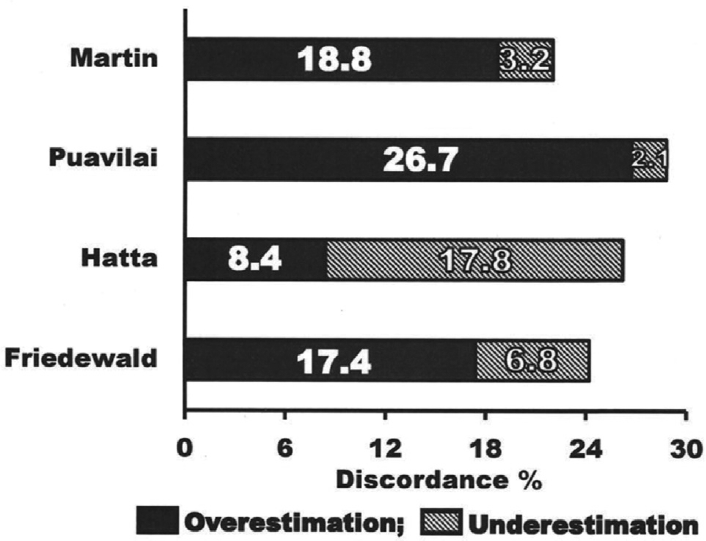
- Overall discordant percentage of LDL-C derived from Friedewald, Hata, Puavilai, and Martin methods. Discordance percentage was derived in comparison with Direct LDL-C cutoff as per NCEP-ATP III guideline.
A gradual declination in concordance percentage and an exacerbation of interpercentile range with increasing TGLs emerged as a common feature among the formula-based methods (►Table 3, ►Supplementary Tables 4 and 5 [available online only], ►Fig. 2). Both LDL-CF and LDL-CH showed gradual transition from overestimation to underestimation. However, predominance of underestimation is the distinct feature of LDL-CH. Though both LDL-CM and LDL-CP overestimated, yet only LDL-CM has shown gradual rise in overestimation with increasing interval of TGLs. Among the four methods, only LDL-CM has narrowest interpercentile range at each stipulated interval of TGL. Both LDL-CM and LDL-CH at TGL < 100 mg/dL; LDL-CM, LDL-CF, and LDL-CH at TGL = 100 to 149 mg/dL interval of TGL; and LDL-CM, LDL-CF, and LDL-CH at TGL > 199 mg/dL exhibited significant indistinguishable concordances. In most of these intervals of TGL, LDL-CM has highest concordance. Especially at 150 to 199 mg/dL interval of TGL, only LDL-CM with higher concordance has shown significant consensus with highest concordance LDL-CF.
![Impact of TGL on formula based LDL-C measurements: absolute difference and post hoc Dunn's test at various TGL intervals as per NCEP-ATP III guidelines. [Absolute difference plot: median with 5th and 95th interpercentile range. Each node in post hoc test: concordant number; dark interconnecting line: significant Bonferroni corrected p-value; dotted line: not significant Bonferroni corrected p-value; and without interconnecting line: p = 1.000. LDL-CC: calculated LDL-C derived from Friedewald (F), Hata (H), Puavilai (P), and Martin (M) formulae; LDL-CD: direct LDL-C; TGL: triglycerides.]](/content/164/2022/14/1/img/JLP-14-065-g002.png)
- Impact of TGL on formula based LDL-C measurements: absolute difference and post hoc Dunn's test at various TGL intervals as per NCEP-ATP III guidelines. [Absolute difference plot: median with 5th and 95th interpercentile range. Each node in post hoc test: concordant number; dark interconnecting line: significant Bonferroni corrected p-value; dotted line: not significant Bonferroni corrected p-value; and without interconnecting line: p = 1.000. LDL-CC: calculated LDL-C derived from Friedewald (F), Hata (H), Puavilai (P), and Martin (M) formulae; LDL-CD: direct LDL-C; TGL: triglycerides.]
| LDL-CF | LDL-CH | LDL-CP | LDL-CM | |||||
|---|---|---|---|---|---|---|---|---|
| C/T | %(95%CI) | C/T | %(95%CI) | C/T | %(95%CI) | C/T | %(95%CI) | |
| Triglycerides, mg/dL | ||||||||
| < 100 | 516/663 | 77.8 (74.7–81.0) | 540/663 | 81.4 (78.5–84.4) | 487/663 | 73.4 (70.1–76.8) | 551/663 | 83.1 (80.2–85.9) |
| 100–149 | 448/578 | 77.5 (74.1–80.9) | 447/578 | 77.3 (73.9–80.7) | 422/578 | 73.0 (69.4–76.6) | 460/578 | 79.6 (76.3–82.9) |
| 150–199 | 212/282 | 75.2 (70.1–80.2) | 187/282 | 66.3 (60.8–71.8) | 188/282 | 66.7 (61.2–72.1) | 198/282 | 70.2 (64.9–75.5) |
| 200–399 | 149/224 | 66.5 (60.3–72.7) | 116/224 | 51.8 (45.2–58.3) | 146/224 | 65.2 (58.9–71.4) | 153/224 | 68.3 (62.2–74.4) |
| Overall | 1325/1747 | 75.8 (73.8–77.9) | 1290/1747 | 73.8 (71.8–75.9) | 1243/1747 | 71.2 (69.0–73.3) | 1362/1747 | 78.0 (76.0–79.9) |
| HDL-C, mg/dL | ||||||||
| < 40 mg/dL | 616/835 | 73.8 (70.8–76.8) | 586/835 | 70.2 (67.1–73.3) | 566/835 | 67.8 (64.6–70.9) | 614/835 | 73.5 (70.5–76.5) |
| 40–59 mg/dL | 590/758 | 77.8 (74.9–80.8) | 578/758 | 76.2 (73.2–79.3) | 559/758 | 73.7 (70.6–76.9) | 627/758 | 82.7 (80.0–85.4) |
| > 60 mg/dL | 119/154 | 77.3 (70.6–83.9) | 126/154 | 81.8 (75.7–87.9) | 118/154 | 76.6 (69.9–83.3) | 121/154 | 78.6 (73.5–86.2) |
| Overall | 1325/1747 | 75.8 (73.8–77.9) | 1290/1747 | 73.8 (71.8–75.9) | 1243/1747 | 71.2 (69.0–73.3) | 1362/1747 | 78.0 (76.0–79.9) |
| TChol, mg/dL | ||||||||
| < 200 mg/dL | 684/856 | 79.9 (77.2–82.6) | 637/856 | 74.4 (71.5–77.3) | 673/856 | 78.6 (75.9–81.4) | 706/856 | 82.5 (79.9–85.0) |
| 200–239 mg/dL | 403/551 | 73.1 (69.4–76.8) | 400/551 | 72.6 (68.9–76.3) | 370/551 | 67.2 (63.2–71.1) | 413/551 | 74.9 (71.3–78.6) |
| > 240 mg/dL | 238/340 | 69.7 (64.8–74.6) | 253/340 | 74.4 (69.8–79.1) | 200/340 | 58.8 (53.6–64.1) | 243/340 | 71.5 (66.7–76.3) |
| Overall | 1325/1747 | 75.8 (73.8–77.9) | 1290/1747 | 73.8 (71.8–75.9) | 1243/1747 | 71.2 (69.0–73.3) | 1362/1747 | 78.0 (76.0–79.9) |
Abbreviations: C/T, concordant number/total number; CI, confidence interval; HDL-C, high-density lipoprotein cholesterol; TChol, total cholesterol. Concordance was designated in accordance to direct LDL-C.; LDL-C, low-density lipoprotein cholesterol; LDL-CF, Friedewald LDL-C; LDL-CH, Hata LDL-C; LDL-CM, Martin LDL-C; NCEP-ATPIII, National Cholesterol Education Program-Adult Treatment Panel III; LDL-CP, Puavilai LDL-C.
In lines of observation with respect to impact of TGL, gradual downfall in concordance percentage as well as exaggeration of interpercentile range was mostly apparent even with increasing intervals of TChol (►Table 3, ►Supplementary Tables 4 and 5[available online only], ►Fig. 3]). Though LDL-CH executed gradual improvement in concordance and steady transition from underestimation to overestimation yet writhed with relatively widest interpercentile range and its further intensification with increasing levels of TChol. The remaining three formulae (LDL-CF, LDL-CP, and LDL-CM) showed gradual escalation in overestimation with the increasing interval of TChol. LDL-CP, in contrast to LDL-CH, showed steady deterioration in concordance. Only LDL-CM had consistent relatively narrowest interpercentile range with lowest median, even at each restricted interval of TChol. LDL-CF also showed competitively higher to high concordance in concurrence with LDL-CM and LDL-CH at their respective highest concordance but suffered with comparatively wider interpercentile range at all levels of TChol.
![Impact of TChol on formula based LDL-C measurements: absolute difference and post hoc Dunn's test at various TChol intervals as per NCEP-ATP III guidelines. [Absolute difference plot: median with 5th and 95th interpercentile range. Each node in post hoc test: concordant number; dark interconnecting line: significant Bonferroni corrected p-value; dotted line: not significant Bonferroni corrected p-value; and without interconnecting line: p = 1.000. LDL-CC: calculated LDL-C derived from Friedewald (F), Hata (H), Puavilai (P), and Martin (M) formulae; LDL-CD: direct LDL-C; TChol: total cholesterol.]](/content/164/2022/14/1/img/JLP-14-065-g003.png)
- Impact of TChol on formula based LDL-C measurements: absolute difference and post hoc Dunn's test at various TChol intervals as per NCEP-ATP III guidelines. [Absolute difference plot: median with 5th and 95th interpercentile range. Each node in post hoc test: concordant number; dark interconnecting line: significant Bonferroni corrected p-value; dotted line: not significant Bonferroni corrected p-value; and without interconnecting line: p = 1.000. LDL-CC: calculated LDL-C derived from Friedewald (F), Hata (H), Puavilai (P), and Martin (M) formulae; LDL-CD: direct LDL-C; TChol: total cholesterol.]
In comparison to TGL and TChol, the interpretations in terms of impact of HDL-C on formula-based methods were quite opposite. With the increasing intervals of HDL-C, there is improvement in concordance percentage and narrowing in interpercentile range (►Table 3, ►Supplementary Tables 4 and ►5[available online only]; ►Fig. 4). At lower interval of HDL-C, both LDL-CF and LDL-CM shared almost equivalent concordance, but LDL-CM outweighs with relatively narrowest interpercentile range. LDL-CP with relatively wide interpercentile had lowest concordance and shown significant difference with LDL-CF and LDL-CM. LDL-CH has not exhibited significant difference with remaining three methods, but suffered with widest interpercentile range and lower concordance. Even at mid-interval of HDL-C, LDL-CM with narrowest interpercentile range expressed significant highest concordance in comparison to remaining three methods. At the upper interval of HDL-C, the impact was alike for all the four approaches. However, only LDL-CM has relatively narrowest interpercentile range.
![Impact of HDL-C on formula based LDL-C measurements: absolute difference and post hoc Dunn's test at various HDL-C intervals as per NCEP-ATP III guidelines. [Absolute difference plot: median with 5th and 95th interpercentile range. Each node in post hoc test: concordant number; dark interconnecting line: significant Bonferroni corrected p-value; dotted line: not significant Bonferroni corrected p-value; and without interconnecting line: p = 1.000. LDL-CC: calculated LDL-C derived from Friedewald (F), Hata (H), Puavilai (P), and Martin (M) formulae; LDL-CD: direct LDL-C; HDL-C: high density lipoprotein cholesterol.]](/content/164/2022/14/1/img/JLP-14-065-g004.png)
- Impact of HDL-C on formula based LDL-C measurements: absolute difference and post hoc Dunn's test at various HDL-C intervals as per NCEP-ATP III guidelines. [Absolute difference plot: median with 5th and 95th interpercentile range. Each node in post hoc test: concordant number; dark interconnecting line: significant Bonferroni corrected p-value; dotted line: not significant Bonferroni corrected p-value; and without interconnecting line: p = 1.000. LDL-CC: calculated LDL-C derived from Friedewald (F), Hata (H), Puavilai (P), and Martin (M) formulae; LDL-CD: direct LDL-C; HDL-C: high density lipoprotein cholesterol.]
Discussion
Accurate estimate of LDL-C even using formula-based approaches is an essential criterion as it decides the treatment strategies for lipid disorders. Therefore, the present study was undertaken to compare the formulae-based methods with fixed and adjustable TG:VLDL ratio. Most of the studies on Indian population evaluated FF and Anandaraja equation.[14,16-19] Correlation, regression, paired t-test, and Bland-Altman plot were traditionally preferred as statistical tools for understanding the agreement between LDL-C and formula-based LDL-C computations in these studies. However, correlation coefficient and regression technique only evaluates the linear association of two sets of observations.[23,24] Paired t-test is efficient only in measuring constant differences but not the other differences as apparent in comparative studies.[23,24] Nevertheless, even the Bland-Altman plots only quantifies limits of agreement (95% of differences between formula-based methods and LDL-C) with bias and percentage error but not assessing the degree of concordance.[23] In view of that, the statistical approach of the present study comprised cross-tabulations for concordance and discordance percentage, median with 5th and 95th interpercentile range for absolute difference between LDL-CD and formula-based LDL-C.
All the three formulae comprising those with extreme end fixed factors (LDL-CH and LDL-CP) as well as with an adjustable factor (LDL-CM) were developed based on computations of TGL:VLDL-C ratio on their respective population with an improved accuracy in comparison to LDL-CF. Although LDL-CH formula was tailored on Japanese population, subsequent validation study on Japanese American recommended LDL-C as more relevant approach.[7] In the same lines, both Thailand group recommended LDL-CP and LDL-CF exhibited a moderate-to-very strong competitive correlation with respect to LDL-C in discrete validation studies of international as well as national groups.[8-11,14] Almost all these studies have demonstrated relatively higher correlation coefficient of LDL-C.[8,9,11,14] However, contrasting observation was revealed in one of the comparative studies on Nigerian population.[10] In their study, moderate correlation of LDL-CP versus LDL-CD < LDL-CF versus LDL-CD. In summary, most of the validation studies concluded that correlation coefficient of LDL-CP > LDL-CF > LDL-C. This hypothesis was further substantiated in one of the validation studies on Korean population.[11] In addition to these three formulae, they had also validated the LDL-CM and concluded that concordance percentage of LDL-CM > LDL-CP > LDL-CF > LDL-CH. Even the present study also further corroborates relatively dominant performance of LDL-C.[9,11] Though the present study is analogous to validation study on Korean population, it provides mixed and distinct inferences. Though the correlation coefficient output of our study corroborates with most of the previous studies[7-9] comprising even validation study on Korean population,[11] holistic interpretations concluded based on concordance and discordance percentage of the present study were preferably in corroboration with outputs of correlation coefficient studies on Japanese-American[7] and Nigerian population,[10] that is, LDL-CF overweighed in comparison to either LDL-CH (or) LDL-CP. As documented in validation study on Korean population, the overestimation was relatively prominent in discordant percentage of only LDL-CP, whereas in our study, it was an apparent feature of three formulae, that is, LDL-CP > LDL-CM > LDL-CF. The overestimation observed in the present study can be attributed to the inability of LDL-C assay to capture all three elements of LDL-C unlike β-quantification.[9] The confounding influence of TChol, TGL, and HDL-C on formulae-based methods was also along the lines of previous studies.[7-19] The mixed performance variation can be attributed to the diversity in ethnicity, dietary, environmental, pathologies, and limitations of the present study.
As it is well known, underestimation in general population screening not only leads to undesirable delay in the initial clinical treatment but also relatively much riskier to overestimation. Hence, LDL-CH with underestimation as a dominant feature may not be the preferred choice. Though overestimation is an apparent feature in the remaining formula-based approaches, LDL-CM outstands with highest concordance percentage and minimal absolute difference with narrowest interpercentile range. However, as overestimation especially in high-risk cardiovascular patients (treatment target of < 70 mg/dL) causes unwarranted intensive prolonged therapeutic regime exacerbating financial and psychological trauma, the choice of formula-based LDL-C measurements in such patients may be clinically dispensable.
The limitations of the current study comprise noninvolvement of β-quantification of LDL-C as gold standard approach and a bias in participant selection based on exclusion criteria. Moreover, owing to the probability of existing characteristic baseline differences between the subjects recruited in the present study and general population, these observations may not be generalizable to the overall population. However, the present study provides an insight into the risk associated with the application of correlation coefficient in method comparison studies. It also demonstrates the necessity of further rigorous validation of these formulae especially LDL-CM method under stringent clinical and laboratory conditions before generalizing to the overall Indian population.
Conclusion
Despite highest concordance of LDL-CH in upper intervals of LDL-C, coexistence of predominance of underestimation with relatively widest interpercentile range raises ambiguity of its application in diagnostic setup. Overestimation is an apparent and common feature in the remaining three methods in the order of LDL-CP > LDL-CM > LDL-CF. However, LDL-CP and LDL-CF comparatively occupied inconsistent intermittent interchangeable positions in terms of concordance percentage and absolute difference computed as median with interpercentile range in the restricted interval analyses of LDL-C. From a holistic point of view, among the four formulae-based approaches, relative predominance of overestimation, high concordance percentage, and consistent narrowest interpercentile range emerged as an attributes of LDL-CM. Even the impact of TChol, TGL, and HDL-C on LDL-CM is relatively minimal. Hence, LDL-CM exhibits the potential as a replacement for the existing popular LDL-CF method in Indian adults.
Acknowledgments
The present work is a part of the institutional project titled “Comparison of formulas for calculating low density lipoprotein cholesterol with homogenous assays.” The author sincerely acknowledges the management of “Karpagam Faculty of Medical Sciences and Research” for their support and encouragement in accomplishing this study. The author also extends sincere thanks to Ms. Sangeetha B for her technical skills in organizing and procuring the laboratory data.
Conflict of Interest
Nil.
References
- Third report of the National Cholesterol Education Program (NCEP) expert panel on detection, evaluation, and treatment of high blood cholesterol in adults (adult treatment panel iii) final report. Circulation. 2002;106(25):3143-3421.
- [CrossRef] [PubMed] [Google Scholar]
- ESC Scientific Document Group. Group ESCSD. 2016 ESC/EAS guidelines for the management of dyslipidaemias. Eur Heart J. 2016;37(39):2999-3058.
- [CrossRef] [PubMed] [Google Scholar]
- Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin Chem. 1972;18(06):499-502.
- [Google Scholar]
- Application of Friedewald's LDL-cholesterol estimation formula to serum lipids in the Japanese population. Jpn Circ J. 1986;50(12):1191-1200.
- [CrossRef] [PubMed] [Google Scholar]
- The accuracy in using modified Friedewald equation to calculate LDL from non-fast triglyceride: a pilot study. J Med Assoc Thai. 2009;92(02):182-187.
- [Google Scholar]
- Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA. 2013;310(19):2061-2068.
- [CrossRef] [PubMed] [Google Scholar]
- Friedewald's LDL-cholesterol estimation formula in a Japanese American population. Jpn Circ J. 1988;52(07):604-606.
- [CrossRef] [PubMed] [Google Scholar]
- Determining a new formula for calculating low-density lipoprotein cholesterol: data mining approach. EXCLI J. 2015;14:478-483.
- [Google Scholar]
- Martins equation as the most suitable method for estimation of low-density lipoprotein cholesterol levels in Korean adults. Korean J Fam Med. 2017;38(05):263-269.
- [CrossRef] [PubMed] [Google Scholar]
- Comparison of calculated versus directly-measured low-density lipoprotein-cholesterol: an evaluation of ten formulas for an HIV-positive population in Sub-Saharan Africa. J Lab Physicians. 2017;9(02):111-115.
- [CrossRef] [PubMed] [Google Scholar]
- Validation of the Martin method for estimating low-density lipoprotein cholesterol levels in Korean: findings from the Korea National Health and Nutritional Examination Survey, 2009–2011. PLoS One. 2016;11(01):e0148147.
- [CrossRef] [PubMed] [Google Scholar]
- Underestimation of low-density lipoprotein cholesterol with the Friedewald equation versus a direct homogenous low-density lipoprotein cholesterol assay. Lab Med. 2017;48(03):220-224.
- [CrossRef] [PubMed] [Google Scholar]
- Comparison of Friedewald formula and modified Friedewald formula with direct homogeneous assay for low density lipoprotein cholesterol estimation. J Coll Physicians Surg Pak. 2014;24(01):8-12.
- [Google Scholar]
- Comparison of LDL-cholesterol estimate using various formulae with directly measured LDL-cholesterol in Indian population. J Clin Diagn Res. 2016;10(12):BC11-BC13.
- [CrossRef] [PubMed] [Google Scholar]
- Comparison of Friedewald's formula and Martin's method with direct assay of serum LDL-cholesterol. Sch J App Med Sci. 2018;6(03):951-959.
- [Google Scholar]
- Current understanding in the measurement of low density lipoprotein cholesterol: A comparison of direct measurement by homogenous assays versus calculations. Int J Clin Biochem Res. 2016;3(02):162-168.
- [CrossRef] [Google Scholar]
- Anandaraja formula or Friedewald formula, which is better formula for calculating LDL-cholesterol in comparison with direct LDL-measurement by homogenous assay method. IJCMR. 2017;2(01):229-231.
- [Google Scholar]
- A leap above Friedewald formula for calculation of low-density lipoprotein cholesterol. J Lab Physicians. 2015;7(01):11-16.
- [CrossRef] [PubMed] [Google Scholar]
- Comparison of Friedewald's and Anandraja's formula with direct estimation of low-density lipoprotein cholesterol in Shivamoga population. IAIM. 2016;3(07):120-131.
- [Google Scholar]
- Methods for measurement of LDL-cholesterol: a critical assessment of direct measurement by homogeneous assays versus calculation. Clin Chem. 2002;48(02):236-254.
- [CrossRef] [PubMed] [Google Scholar]
- Impact of nutrients and food components on dyslipidemias: what is the evidence? Adv Nutr. 2015;6(06):703-711.
- [CrossRef] [PubMed] [Google Scholar]
- Effects of dietary macronutrients on plasma lipid levels and the consequence for cardiovascular disease. J Cardiovasc Dev Dis. 2014;1:201-213.
- [CrossRef] [Google Scholar]
- Understanding Bland Altman analysis. Biochem Med (Zagreb). 2015;25(02):141-151.
- [CrossRef] [PubMed] [Google Scholar]
- Design, analysis, and interpretation of method-comparison studies. AACN Adv Crit Care. 2008;19(02):223-234.
- [CrossRef] [PubMed] [Google Scholar]





