Translate this page into:
How to Analyze the Diagnostic Performance of a New Test? Explained with Illustrations
Address for correspondence: Deepak Dhamnetiya, MD, Department of Community Medicine, Dr Baba Saheb Ambedkar Medical College and Hospital, Sector-6, Rohini, Delhi, 110085, India (e-mail: drdeepakdhamnetiya@gmail.com).
This article was originally published by Thieme Medical and Scientific Publishers Pvt. Ltd. and was migrated to Scientific Scholar after the change of Publisher.
Abstract
Diagnostic tests are pivotal in modern medicine due to their applications in statistical decision-making regarding confirming or ruling out the presence of a disease in patients. In this regard, sensitivity and specificity are two most important and widely utilized components that measure the inherent validity of a diagnostic test for dichotomous outcomes against a gold standard test. Other diagnostic indices like positive predictive value, negative predictive value, positive likelihood ratio, negative likelihood ratio, accuracy of a diagnostic test, and the effect of prevalence on various diagnostic indices have also been discussed. We have tried to present the performance of a classification model at all classification thresholds by reviewing the receiver operating characteristic (ROC) curve and the depiction of the tradeoff between sensitivity and (1–specificity) across a series of cutoff points when the diagnostic test is on a continuous scale. The area under the ROC (AUROC) and comparison of AUROCs of different tests have also been discussed. Reliability of a test is defined in terms of the repeatability of the test such that the test gives consistent results when repeated more than once on the same individual or material, under the same conditions. In this article, we have presented the calculation of kappa coefficient, which is the simplest way of finding the agreement between two observers by calculating the overall percentage of agreement. When the prevalence of disease in the population is low, prospective study becomes increasingly difficult to handle through the conventional design. Hence, we chose to describe three more designs along with the conventional one and presented the sensitivity and specificity calculations for those designs. We tried to offer some guidance in choosing the best possible design among these four designs, depending on a number of factors. The ultimate aim of this article is to provide the basic conceptual framework and interpretation of various diagnostic test indices, ROC analysis, comparison of diagnostic accuracy of different tests, and the reliability of a test so that the clinicians can use it effectively. Several R packages, as mentioned in this article, can prove handy during quantitative synthesis of clinical data related to diagnostic tests.
Keywords
diagnostic study
sensitivity
specificity
ROC curve
kappa statistics
diagnostic accuracy
Introduction
Diagnostic testing can be used to discriminate subjects with a target disorder from subjects without it.[1] Diagnostic information is obtained from a multitude of sources, including imaging and biochemical technologies, pathological and psychological investigations, and signs and symptoms elicited during history taking and clinical examinations.[2] Most diagnostic studies focus on diagnostic test accuracy (DTA), which expresses a test's ability to discriminate between people with the target condition and those without it.[3] The most commonly used measures of accuracy or validity are sensitivity and specificity. Sensitivity refers to its ability to detect a high proportion of the true cases, that is, to yield few false negative results. Specificity on the other hand refers to the fact that a specific test is the one that correctly identifies the true negative, and hence yields few false positive verdicts.[4] The whole point of diagnostic test is to use it to make a diagnosis, so we need to know the probability that the test will give the correct diagnosis. The sensitivity and specificity do not give us this information. Instead, we must approach the data from the direction of the test results, using predictive values. The probability of disease, given the result of a test is called the predictive value of the test.[5] Positive predictive value (PPV) is the probability that a subject with a positive screening test is actually suffering from the disease. Negative predictive value (NPV) on the other hand is the probability that a subject diagnosed by a negative screening test result truly do not have the disease in reality. Hence, both the predictive values are associated with the diagnosis being correct.[6] However, predictive value of the test depends on prevalence of the disease. Another useful measure of the accuracy of a diagnostic test is the likelihood ratio (LR). LR indicates the value of the test for increasing certainty about a positive diagnosis. For any test results we can compare the probability of getting that result if the patient truly had the condition of interest with the corresponding probability of he or she were healthy. The ratio of these two probabilities is called the LR.[5-7] Odds ratio is also one global measure for diagnostic accuracy, used for general estimation of discriminative power of diagnostic procedures and also for the comparison of diagnostic accuracies between two or more diagnostic tests.[1] Another index named as Youden's index is one of the oldest measures for diagnostic accuracy. It is also a global measure of a test performance, used for the evaluation of overall discriminative power of a diagnostic procedure.[8] Next, we have the receiver operating characteristic (ROC) curve which is nothing but the plot that displays the full picture of tradeoff between the sensitivity and (1–specificity) across a series of cutoff points. Area under the ROC (AUROC) curve is considered as an effective measure of inherent validity of a diagnostic test. This curve is useful in (1) finding optimal cutoff point to least misclassify diseased or nondiseased subjects, (2) evaluating the discriminatory ability of a test to correctly pick diseased and nondiseased subjects, (3) comparing the efficacy of two or more tests for assessing the same disease, and (4) comparing two or more observers measuring the same test (interobserver variability).[9] Finally, we look into reliability of a test as the repeatability of the test, that is, the test must give consistent results when repeated more than once on the same individuals, under the same conditions. The simplest way of finding the agreement between the two researchers or clinicians is to calculate overall percentage of agreement. However, neither of these measures takes into account of the agreement that would be expected purely by chance. If clinicians agree purely by chance, they are not really “agreeing” at all; only agreement beyond that expected by chance can be considered as “true” agreement. For analyzing such kind of data, the kappa coefficient is an appropriate measure of reliability. It is a measure of “true” agreement beyond that expected by chance.[10]
Problem statement: Suppose a cross-sectional study is conducted to know the diagnostic accuracy of new screening test X to detect disease A. The prevalence of the disease A is found to be 40%. In a sample of 200 subjects, test X detects 69 subjects with presence of disease out of total actually having disease and 95 subjects with no disease out of total nondiseased. We will find all the possible indices as mentioned in the earlier section.
Solution: First step in diagnostic studies is to construct the 2 × 2 table.
Basic concepts to keep in mind before constructing 2 × 2 tables: Reference test/Confirmatory test/Gold standard test/True disease status will be represented in columns and screening test/new test will be represented in rows (►Table 1).
| Disease | ||||
|---|---|---|---|---|
| Present | Absent | Total | ||
| Screening test/New test | Positive | a (true positive) | b (false positive) | a + b |
| Negative | c (false negative) | d (true negative) | c + d | |
| Total | a + c | b + d | N | |
Information given in the problem:
Prevalence = 40%
Total Subject (N) = 200
No. of subjects test X detects as diseased = 69
No. of subjects test X detects as nondiseased = 95
As the prevalence of the diseased in the population is 40%. Hence, from this information we can calculate the actual number of diseased in given data.

which gives the total number of persons who truly are suffering from the disease = 80.
Total number of persons who are not suffering from the diseases = 200–80 = 120.
Now, let us construct 2 × 2 tables from the above calculated information (►Table 2) and then we calculate the values of the other indices.
| Disease | ||||
|---|---|---|---|---|
| Present | Absent | Total | ||
| Test X | Positive | 69 | 25 | 94 |
| Negative | 11 | 95 | 106 | |
| Total | 80 | 120 | 200 | |
Sensitivity (Sn): As mentioned earlier, it is the ability of the test to detect true positives or proportion of people with the disease who have a positive test. Sensitivity is calculated as

Sensitivity, in this problem is, 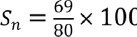 , that is, 86.25% (76.73–92.93%). Please note that the confidence intervals for sensitivity is “exact” Clopper–Pearson confidence intervals.
, that is, 86.25% (76.73–92.93%). Please note that the confidence intervals for sensitivity is “exact” Clopper–Pearson confidence intervals.
Interpretation: The new diagnostic/screening test X is able to detect 86.25% of the actual diseased among total diseased, if used as screening test for disease A.
Specificity (Sp): It is the ability of a test to detect true negatives or proportion of people without the disease who have a negative report of the screening test. Specificity is calculated as
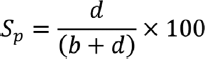
Specificity, in this case is,  , that is, 79.17% (70.80–86.04%).
, that is, 79.17% (70.80–86.04%).
Confidence intervals for specificity are again the “exact” Clopper–Pearson confidence intervals.
Interpretation: The new diagnostic test X is able to detect 79.17% of the actual nondiseased among total nondiseased, when used as a screening test for disease A.
PPV: PPV is the probability of having disease in a patient with a positive test result. PPV is calculated as

Here, we have,  , that is, 73.40% (65.83–79.82%).
, that is, 73.40% (65.83–79.82%).
The confidence intervals for the predictive values are the standard logit confidence intervals.[11]
Interpretation: For a subject with positive new diagnostic test X results, the probability of the subject truly having the disease A is 73.40%.
NPV: NPV on the other hand is the probability of not having disease in a patient with a negative test result. NPV is calculated as
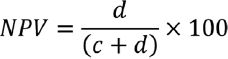
And we get,  , that is, 89.62% (83.20–93.78%).
, that is, 89.62% (83.20–93.78%).
Confidence intervals for the predictive values are the standard logit confidence intervals.[11]
Interpretation: For a subject with negative new diagnostic test X results, the probability of the subject truly not having the disease A is 89.62%.
LR: It indicates the value of the test for increasing certainty about a positive diagnosis. It is the ratio of probability of getting the test result in subjects with the disease and subjects without the disease.
Positive LR (LR +): It is the ratio of probability of getting the positive test result in subjects with the disease to the subjects without the disease.
LR+ is calculated as sensitivity/(1–specificity) or true positive rate/false positive rate

Confidence intervals for the LRs are calculated using the “log method.”[12]
Interpretation: The probability of getting +ve test X result in truly diseased is 4.14 times vis-à-vis nondiseased.
Negative LR (LR–): LR– is the ratio of probability of getting the negative test result in subjects with the disease to the subjects without the disease.
LR– is calculated as (1–specificity)/specificity or false negative rate/true negative rate

Confidence intervals for the LRs are calculated using the “log method.”[12]
Interpretation: The probability of getting –ve test X result in truly diseased is 0.17 times vis-à-vis nondiseased.
Accuracy: It is the overall probability that a patient is correctly classified
= (Sensitivity × Prevalence) + Specificity × (1 − Prevalence)
= 82.00% (75.96–87.06%)
Confidence intervals for accuracy are the “exact” Clopper–Pearson confidence intervals.
Interpretation: The probability of getting a subject correctly classified as diseased or nondiseased by the test X is 0.82 (82%).
Youden's index: It is calculated by deducting 1 from the sum of test's sensitivity and specificity expressed not as percentage but as a part of a whole number, that is, Youden's index = (sensitivity + specificity) – 1. For a test with poor diagnostic accuracy, Youden's index equals 0, and in case of a perfect test, Youden's index is 1.[8]
In the abovementioned example the sensitivity of the test X is 86.25% and specificity is 79.17%.
Therefore, Youden's index = (sensitivity + specificity) – 1 = (0.863 + 0.791) – 1
Youden's index = 0.654.
Interpretation: Diagnostic accuracy of screening test X to detect the disease A in patients is moderate as it is just above 50%.
Here, we will discuss the effect of prevalence of disease on various diagnostic indices using same example.
►Table 3 shows that there is no effect of prevalence on sensitivity, specificity, LR +, and LR–. PPV and accuracy are directly associated with the prevalence of the disease whereas NPV is inversely associated.
| Prevalence (%) | Sensitivity | Specificity | LR+ | LR– | PPV | NPV | Accuracy |
|---|---|---|---|---|---|---|---|
| 20 | 86.25 | 79.17 | 4.14 | 0.17 | 50.86 | 95.84 | 80.58 |
| 30 | 86.25 | 79.17 | 4.14 | 0.17 | 63.95 | 93.07 | 81.29 |
| 40 | 86.25 | 79.17 | 4.14 | 0.17 | 73.40 | 89.62 | 82.00 |
| 50 | 86.25 | 79.17 | 4.14 | 0.17 | 80.54 | 85.20 | 82.71 |
| 60 | 86.25 | 79.17 | 4.14 | 0.17 | 86.13 | 79.33 | 83.42 |
Abbreviations: LR, likelihood ratio; NPV, negative predictive value; PPV, positive predictive value.
Section II: In this section we will discuss ROC curve which is widely used to decide cutoff value for test X1 having continuous outcome and to compare the diagnostic accuracy of three different tests (X1, X2, and X3).
ROC curve: When the cutoff value for a continuous diagnostic variable is increased (assuming that larger values indicate an increased chance of a positive outcome), the proportions of both true and false positives decreases. These proportions are the sensitivity and 1–specificity, respectively. A graph of sensitivity against 1–specificity is what we call a ROC curve.
Each point on the ROC curve represents a different cutoff value. The points are connected to form the curve. For a test, cutoff values that result in low false positive rates tend to have low true positive rates (and hence low in power) as well. As the true positive rate increases, the false positive rate increases. The better the diagnostic test, the more quickly the true positive rate nears 1 (or 100%). A near-perfect diagnostic test would have an ROC curve that is almost vertical from (0,0) to (0,1) and then horizontal to (1,1). The diagonal line serves as a reference line since it is the ROC curve of a diagnostic test that randomly classifies the condition (►Fig. 1).

- Receiver operator characteristics curve of test X1 for diagnosing disease A.
While the ROC curve together with the corresponding area under the curve (AUC) gives an overall picture of the behavior of a diagnostic test across all cutoff values, there remains a practical need to determine the specific cutoff value that should be used to determine the best screening test for individuals requiring diagnosis. In this case, a recommended approach is to find the cutoff with highest Youden's index, or equivalently, the highest sensitivity + specificity.[13]
The left top most point on the ROC curve indicates the highest Youden's index for any given diagnostic test. After that point the sensitivity will slightly increase, but we have to compromise with the specificity. However, sometimes specific objective of the diagnostic test is used to decide the cutoff. In our example, red dot on the ROC curve represents the test with highest Youden's index.
AUROC curve: The AUROC curve gives an overall summary of the diagnostic accuracy. The performance of a diagnostic variable can be quantified by calculating the AUROC curve. If AUROC equals 0.5, the ROC curve corresponds to random chance, and on the contrary, AUROC value 1.0 signifies perfect accuracy. On rare occasions, the estimated AUROC is < 0.5, which indicates that the test has actually performed worse than chance.[14]
For continuous diagnostic data, the nonparametric estimate of AUROC is nothing but the Wilcoxon rank-sum test, which is defined as the proportion of all possible pairs of nondiseased and diseased test subjects for which the diseased result is higher than the nondiseased one plus half the proportion of ties.
In our example the AUC is found to be 0.849 (∼85%), which is considered as good for a diagnostic test X1 to diagnose disease A. At the cutoff point where the Youden's index is highest, that is, 0.571, the sensitivity and specificity of test X1 to diagnose the disease A is 63.33% and 93.75%, respectively.
Precision-Recall Curves
Precision is a metric that quantifies the number of correct positive predictions made. It is calculated as the number of true positives divided by the total number of true positives and false positives.
Precision = True positives / (true positives + false positives)
The result is a value between 0 and 1. Note that 0 stands for no precision and 1.0 signifies full or perfect precision.
Recall is a metric that quantifies the number of correct positive predictions made out of all positive predictions that could have been made. It is calculated as the number of true positives divided by the total number of true positives and false negatives (e.g., it is the true positive rate).
Recall = True positives / (true positives + false negatives)
The result is a value between 0.0 (for no recall) and 1.0 (for full or perfect recall).
Both the precision and the recall are focused on the positive class (the minority class) and are unconcerned with the true negatives (majority class).
The precision-recall curve shows the tradeoff between precision and recall for different threshold. A high value of area under the abovementioned curve represents both high recall and high precision, here high precision relates to a low false positive rate, and high recall relates to a low false negative rate. High scores for both show that the classifier is returning accurate results (high precision), as well as returning a majority of all positive results (high recall).
This curve focuses mainly on the performance of the positive class which is crucial when dealing with imbalanced classes. In the precision-recall (PR) space, the goal is to be in the upper-right-hand corner—the top right corner (1, 1) means that we classified all positives as positive (Recall = 1) and that everything we are classifying as positive is true positive (Precision = 1)—the latter translates to zero false positives. We have plotted precision-recall curve for diagnostic test X1 (►Fig. 2).

- Precision–recall curve of diagnostic test X1 for disease A.
Comparing Different Tests
When we have two or more different screening tests to diagnose a specific disease, the best way of determining the better screening test is by comparing the diagnostic accuracy of these tests is by making ROC curve and comparing the AUROCs. The larger AUC indicates better diagnostic accuracy of that test as compared to the other with lower AUROCs. Here, we compare diagnostic accuracy of test X1, X2, and X3 to diagnose disease A.
In our example, the ROC has been plotted for all the three screening tests to check the diagnostic accuracy by using AUROCs. The “black dot” on each ROC indicates the cutoff point for that test where the respective Youden's index is highest (►Fig. 3).

- Receiver operator characteristics curve of test X1, X2, and X3 for diagnosing disease A.
The AUC is found to be 0.849 (∼85%), 0.728 (73%), and 0.684 (68.4%) for test X1, X2, and X3, respectively. As the AUC is largest for test X1 among all the three tests, hence we draw inference that the test X1 has better diagnostic accuracy as compared to tests X2 and X3 (►Table 4).
| Variable | Youden's index J | Sensitivity (%) | Specificity (%) | LR+ | LR– | AUC (95% CI) |
|---|---|---|---|---|---|---|
| X1 | 0.571 | 63.333 | 93.75 | 10.133 | 0.391 | 0.849 (0.763, 0.913) |
| X2 | 0.379 | 81.667 | 56.25 | 1.867 | 0.326 | 0.728 (0.629, 0.812) |
| X3 | 0.271 | 85.833 | 41.25 | 1.461 | 0.343 | 0.684 (0.583, 0.773) |
Abbreviations: AUC, area under the curve; AUROC, area under the receiver operating characteristic; CI, confidence interval; LR, likelihood ratio.
Further, Z statistics can be computed to check the difference between the AUROC curves among different test pairwise. In our example, we found that the AUROCs differ significantly among tests X1 and X2 and X1 and X3. However, we have not found any significant difference of AUROCs among test X2 and X3 (►Table 5).
| Comparison | AUC difference | SE | Z-statistic | p-Value |
|---|---|---|---|---|
| X1 and X2 | 0.121 | 0.038 | 3.214 | 0.001 |
| X1 and X3 | 0.165 | 0.04 | 4.175 | < 0.001 |
| X2 and X3 | 0.044 | 0.048 | 0.912 | 0.362 |
Abbreviations: AUC, area under the curve; AUROC, area under the receiver operating characteristic; SE, standard error.
Reliability of a test: The Cohen's kappa is a statistical coefficient that represents the degree of accuracy and reliability in a statistical classification. It measures the agreement between two observers/clinicians who each classifies items into mutually exclusive categories.
The kappa statistics can be calculated by applying this formula:
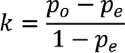
where po is the relative observed agreement among observers, and pe is the hypothetical probability of chance agreement.[15]
Kappa is always less than or equal to 1. A value of 1 implies perfect agreement and values less than 1 imply less than perfect agreement. It is possible that kappa is negative. This only means that the two observers agreed less than what expected under the presence of chance only.
The value of the kappa coefficient can be interpreted from the following table:
Kappa Value Agreement Interpretation
0.01–0.20 slight agreement
0.21–0.40 fair agreement
0.41–0.60 moderate agreement
0.61–0.80 substantial agreement
0.81–1.00 almost perfect or perfect agreement
Let there are two observers. In a sample of 200 subjects, for 86 subjects both the observer diagnosed the person as diseased, there are 12 subjects who were diagnosed as diseased by observer 2 but were screened as nondiseased by observer 1. In case of the other 14 subjects, observer 1 gave the diagnosis as diseased but by observer 2 the diagnosis was opposite, and then there are 88 subjects who were diagnosed as nondiseased by both the observer.
For the abovementioned problem, we can formulate the table as ►Table 6.
| Observer 1 | Total | |||
|---|---|---|---|---|
| Diseased | Nondiseased | |||
| Observer 2 | Diseased | 86 (49) | 12 (51) | 98 |
| Nondiseased | 14 (49) | 88 (51) | 102 | |
| Total | 100 | 100 | 200 | |
In ►Table 6, the observed frequency for agreement among observer 1 and observer 2 is given. Now, we have to calculate the expected frequency for each cell in order to calculate the expected agreement among the observer. The formula to calculate the expected cell frequency is given by:

So, in our example, we see that the kappa coefficient is 0.74 which refers to the fact that there is substantial or good agreement between observer 1 and observer 2.
Diagnostic Test with Low Prevalence Rate
Prospective studies of DTA have important advantages over retrospective designs. Yet, when the disease being detected by the diagnostic test(s) has a low prevalence rate, a prospective design can require an enormous sample of patients. We consider two strategies to reduce the costs of prospective studies of binary diagnostic tests: stratification and two-phase sampling. Utilizing neither, one, or both of these strategies provides us with four study design options: (1) the conventional design involving a simple random sample (SRS) of patients from the clinical population; (2) a stratified design where patients from higher-prevalence subpopulations are more heavily sampled; (3) a simple two-phase design using a SRS in the first phase and selection for the second phase based on the test results from the first; and (4) a two-phase design with stratification in the first phase.[16] The estimation techniques for sensitivity and specificity for each design will be discussed in the next section.
In conventional design, a SRS of patients is taken from the population and all patients are tested and verified. The number of patients with and without the disease is determined. Then we determine the number of positive test results in patients with disease and negative test results in patients without disease. We calculate the specificity and sensitivity using the usual definition.
During the design phase of the study, suppose the investigators are aware of the existence of a subpopulation(s) with a higher prevalence of disease. If it is possible to stratify the clinical population based on the prevalence of disease, then the primary factors influencing the savings afforded by the second design mentioned above are (1) the difference in prevalence rates between the strata, and (2) the relative frequency of the strata in the population. Test's sensitivity and specificity in the population will be determined by a few steps. The investigator first estimates the sensitivity and specificity in each stratum. Then, the estimate of the test's sensitivity for the population is a weighted average of these estimates of stratum-wise sensitivities, population proportion of all diseased patients belonging to the corresponding stratum being the respective weights. Similarly, the test's specificity for the population is determined from the weighted average of these estimates of stratum-wise specificities, where the associated weights are the population proportions of all nondiseased patients belonging to the corresponding stratum.
Next, we will discuss about the simple two-phase design for a single diagnostic test, which was third on our list. Under this scheme, a random sample of patients undergoes the diagnostic test. The investigator considers the case where the investigator verifies all patients who test positive and a random sample of size f × total of the patients who test negative. This fraction “f” plays an important role in derivation of the sensitivity and specificity estimates for the test. If we have a 2 × 2 layout as shown in ►Table 7,
| T = 1 | T = 0 | Total | |
|---|---|---|---|
| D = 1 | s1 | s0 | m1 |
| D = 0 | r1 | r0 | m0 |
where D = 1 and 0 denote the true disease status (diseased and nondiseased, respectively);
T = 1 and 0 denote the test results (positive and negative, respectively),
the sensitivity is given the formula, 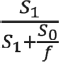
and the specificity is given by, 
There are certain criteria based on which we prefer this design over the previous two. The simple two-phase design is preferred when (1) the test's sensitivity is only moderate at best (< 70%), (2) the specificity is considerably high (> 80%), and (3) the cost of verifying patients is much greater than the cost of testing. Even under these ideal situations, the savings over a conventional design are only modest, usually < 15%. However, this method offers more advantages while we compare two tests.
As we move towards the last design in our list, we need to clarify that the situations in which a stratified design are effective are quite different from the set of circumstances in which a two-phase design is effective. These two strategies, thus, can be used in complementary roles. The two-phase design with stratification in the first phase, for that matter, offers a savings exceeding that of any other design as long as the cost of verifying patients is much greater than the cost of testing. The estimation of sensitivity and specificity is done by using the methods utilized by previous two methods. First, in each stratum we need to verify the disease status of all patients who test positive and a random sample of size f × number of the patients who test negative. For simplicity purpose, we keep f constant in each stratum. Let V(i) denote the number of patients verified from the ith stratum. For each stratum, we use the estimators of sensitivity and specificity as mentioned in the third design. Then, the accuracy for the population can be estimated using the estimators which are aggregated using weighted averages as described in the second design.[16] We found these estimators of accuracy to be equivalent to Begg and Greenes' estimators for the case of stratified data.[17]
Available R Packages for Diagnostic Test Accuracy
Next, we mention quantitative synthesis of data using R software for the general approaches of DTA. We need to conduct a DTA so that we get statistical summaries for both univariate analysis and bivariate analysis. The package commands of R software that can be used are “metaprop” and “metabin” for sensitivity, specificity, and diagnostic odds ratio; forest for forest plot; reitsma of “mada” for a summarized ROC curve; and “metareg” for meta-regression analysis.[18] In addition to the above, the estimated total effect sizes, test for heterogeneity and moderator effect, and a summarized ROC curve can also be reported using R software. Another important R package that can be used is, DTComPair.[19] This package is mainly used for comparing binary diagnostic tests in a paired study design. This package contains functions to compare the accuracy of two binary diagnostic tests in a “paired” study design, that is, when each test is applied to each subject in the study. The calculation of accuracy measures and their variances follows standard methodology, for example, described in these studies.[20,21] CompareTests is another standard R package to estimate agreement and diagnostic accuracy statistics for two diagnostic tests when one is conducted on only a subsample of specimens. A standard test is observed on all specimens. Here, the second test (or sampled test) is treated as being conducted on only a stratified sample of specimens. The total sample is treated as stratified two-phase sampling and then inverse probability weighting is used. Using the functions of this package, the clinicians can estimate diagnostic accuracy (category-specific classification probabilities; for binary tests reduces to specificity and sensitivity, and also predictive values) and agreement statistics (percent agreement, percent agreement by category, kappa [unweighted], and symmetry tests [reduces to McNemar's test for binary tests]) with ease.[22]
Conclusion
DTA studies are particularly difficult to design because of the many sources of bias that are inflicted in these studies.[23,24] If a clinician comes across any new diagnostic test having categorical outcome, they should calculate sensitivity, specificity, PPV, NPV, LR +, LR–, Youden's index, and accuracy to know the diagnostic accuracy of the test. In order to know the cutoff value for the test having continuous outcome, left top most point on the ROC curve should be taken. To compare the diagnostic accuracy of two or more tests, AUROC curve of all the tests shall be calculated. The diagnostic/screening test having higher value of AUROC curve can be expected to provide better accuracy than the other existing tests. We also have showed how kappa statistics is used to compare the interobserver variability and thus makes the statistical decision making simplified. We have also presented how prospective studies are especially difficult when the prevalence of disease in the population is low. We described the sensitivity and specificity calculations for some proposed designs that can deal with the problem. We have also tried to provide some guidance in choosing the best possible design among them, depending on a number of factors. Choosing a study design for diagnostic accuracy studies in low-prevalence situations should be driven by whether the aim is to limit the number of patients undergoing the index test or reference or standard, and the risk of bias associated with a particular design type. Several R packages, as mentioned in this article, can prove handy during quantitative synthesis of clinical data related to diagnostic tests.
Conflict of Interest
None declared.
References:
- The diagnostic odds ratio: a single indicator of test performance. J Clin Epidemiol. 2003;56(11):1129-1135.
- [CrossRef] [PubMed] [Google Scholar]
- Systematic reviews in health care: systematic reviews of evaluations of diagnostic and screening tests. BMJ. 2001;323(7305):157-162.
- [CrossRef] [PubMed] [Google Scholar]
- Cochrane diagnostic test accuracy reviews. Syst Rev. 2013;2:82.
- [CrossRef] [PubMed] [Google Scholar]
- Variation of sensitivity, specificity, likelihood ratios and predictive values with disease prevalence. Stat Med. 1997;16(09):981-991.
- [CrossRef] [Google Scholar]
- Diagnostic tests. 1: sensitivity and specificity. BMJ. 1994;308(6943):1552.
- [CrossRef] [PubMed] [Google Scholar]
- Clinical Epidemiology: The Essentials. (4th). Baltimore: MA: Lippincott Williams and Wilkins; 2005.
- [Google Scholar]
- The systematic review of studies of diagnostic test accuracy, Joanna Briggs Institute Reviewers' Manual. 2015 edition/Supplement
- [Google Scholar]
- Receiver operating characteristic (ROC) curve for medical researchers. Indian Pediatr. 2011;48(04):277-287.
- [CrossRef] [PubMed] [Google Scholar]
- The kappa statistic in reliability studies: use, interpretation, and sample size requirements. Phys Ther. 2005;85(03):257-268.
- [CrossRef] [PubMed] [Google Scholar]
- Confidence intervals for predictive values with an emphasis to case-control studies. Stat Med. 2007;26(10):2170-2183.
- [CrossRef] [PubMed] [Google Scholar]
- Statistical guidelines for contributors to medical journals. In: Altman DG, Machin D, Bryant TN, Gardner MJ, eds. Statistics with Confidence: Confidence Intervals and Statistical Guidelines (2nd). London: BMJ Books; 2000. p. :171-190.
- [Google Scholar]
- ROC Curves for Continuous Data. (1st). Chapman and Hall: CRC; 2009. Accessed on August 16 at https://doi.org/10.1201/9781439800225
- [CrossRef] [PubMed] [Google Scholar]
- The meaning and use of the area under a ROC curve. Radiology. 1982;143:27-36.
- [CrossRef] [PubMed] [Google Scholar]
- The measurement of observer agreement for categorical data. Biometrics. 1977;33(01):159-174.
- [CrossRef] [PubMed] [Google Scholar]
- Prospective studies of diagnostic test accuracy when disease prevalence is low. Biostatistics. 2002;3(04):477-492.
- [CrossRef] [PubMed] [Google Scholar]
- Assessment of diagnostic tests when disease verification is subject to selection bias. Biometrics. 1983;39(01):207-215.
- [CrossRef] [PubMed] [Google Scholar]
- Diagnostic test accuracy: application and practice using R software. Epidemiol Health. 2019;41:e2019007.
- [CrossRef] [PubMed] [Google Scholar]
- Comparison of binary diagnostic tests in a paired study design. Comprehensive R Archive Network website Accessed on August 16 at cran.r-project.org/web/packages/DTComPair/DTComPair.pdf. Published February 2014 15
- [Google Scholar]
- The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford: UK: Oxford University Press; 2003.
- [CrossRef] [Google Scholar]
- Statistical Methods in Diagnostic Medicine. In: Wiley Series in Probability and Statistics (2nd). Hoboken, New Jersey: John Wiley & Sons; 2011.
- [CrossRef] [Google Scholar]
- Estimating the agreement and diagnostic accuracy of two diagnostic tests when one test is conducted on only a subsample of specimens. Stat Med. 2012;31(05):436-448.
- [CrossRef] [PubMed] [Google Scholar]
- Biases in the assessment of diagnostic tests. Stat Med. 1987;6(04):411-423.
- [CrossRef] [PubMed] [Google Scholar]
- Use of methodological standards in diagnostic test research. Getting better but still not good. JAMA. 1995;274(08):645-651.
- [CrossRef] [Google Scholar]






